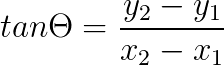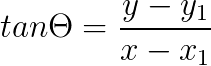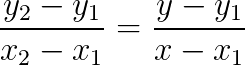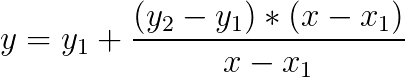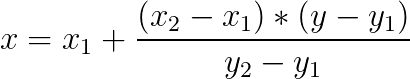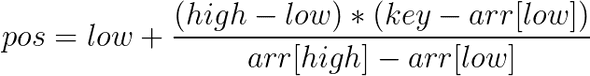Smelly Code

Demystifying Interpolation formula for Interpolation Search

January 19, 2018 ∙ 👨🏻‍💻 4 min

Interpolation Search is similar to Binary Search. In Binary Search, we always calculate middle of the array and compare it with the key. If the key is equal to mid then we return otherwise we reduce our array to subarray based on our comparison. But, with Interpolation Search, instead of calculating the mid, we apply interpolation formula on our uniformly distributed array/input to calculate the nearest position to the key. As mentioned on GeeksforGeeks,

the idea of the formula is to return higher value of position when the element to be searched is closer to the end of the array OR to return smaller value of the position when the element to be searched is closer to the beginning of the array.

Let’s consider a real-life example to grok it better. Suppose you want to search “Yoyo” in a dictionary. If you follow traditional binary search, you’ll flip to the middle of the dictionary and lexically compare the word “Yoyo” with the middle word. But if you apply interpolation search, you’ll flip directly somewhere closer to the end of the dictionary since you know that word “Yoyo” will be closer to the end.

Derivation

To understand the formula let’s derive it. Suppose we have a linear function y = f(x) where the relationship between y and x is defined in the diagram below.

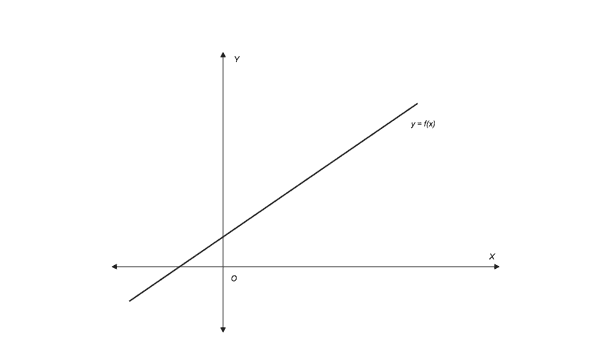
linear function
Linear Function y = f(x).

Consider two points (x1, y1) and (x2, y2) where y1 = f(x1) and y2 = f(x2) ∀ x1 < x2. Let’s place them somewhere on the graph.

linear function 2
y = f(x) with (x1, y1) and (x2, y2)

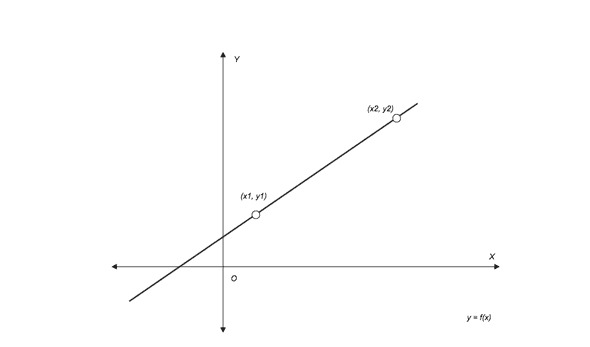
Suppose we want to find an x where x1 <= x <= x2 for a given value of y such that y = f(x). How can we find it? We can use trigonometry.

interpolation formula cover img
Deriving Interpolation Formula with Trigonometry

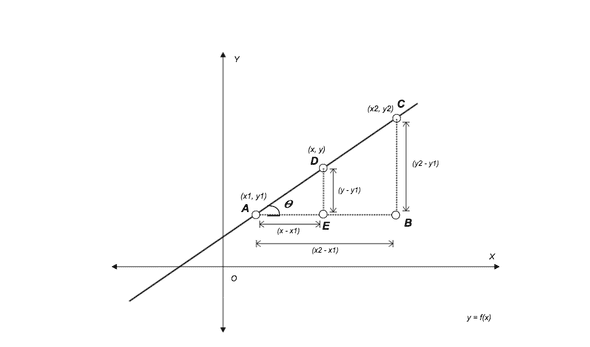
As depicted in the diagram above, the value of tan𝛳 for △ABC will be equal to the value of tan𝛳 for △ADE. From trigonometry, we know that

tangent

It means tan𝛳 for △ABC is:

tangent 1

And tan𝛳 for △ADE is:

tangent 2

Since angle 𝛳 is same for both triangles. Therefore, we can say

tangent 3

which implies that

interpolation formula 1

Or we can say that

interpolation formula 2

Let’s see how this formula can help us to find mid for interpolation search. If we consider our input array as a function f(x) then

x1 => low and y1 => array[low]
x2 => high and y2 => array[high]
x => pos and y => array[pos] i.e. key.

After putting these values in formula

interpolation formula

Here’s the implementation of Interpolation Search in JavaScript.

const interpolationSearch = (array, key) => {
  // if array is empty.
  if (!array.length) {
    return -1;
  }

  let low = 0;
  let high = array.length - 1;
  while (low <= high && key >= array[low] && x <= array[high]) {
    // calculate position with
    let pos =
      low +
      Math.floor(
        ((high - low) * (key - array[low])) / (array[high] - array[low])
      );

    // if all elements are same then we'll have divide by 0 or 0/0
    // which may cause NaN
    pos = Number.isNaN(pos) ? low : pos;

    if (array[pos] === key) {
      return pos;
    }

    if (array[pos] > key) {
      high = pos - 1;
    } else {
      low = pos + 1;
    }
  }

  // not found.
  return -1;
};

Hi, I am Hitesh.

|