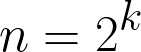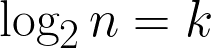Binging Binary Search 🔎
January 09, 2018 ∙ 👩🏻🏫 8 min
Data Structures and Algorithms(DSA) is one of the essential tools which every engineer should have in his/her arsenal. Generally, they are taught in the first year of engineering but, in my first year, I was busy in making “binary trees” 🙂. Because of that, I couldn’t focus on learning and started blindly toying with them. But for 2018, I’ve made a resolution that I will tame this demon of DSA and will not let it haunt me every time I try to step out of my comfort zone. So I’ve started studying DSA and it looks like it’s a long journey but as we know:
“The journey of a thousand miles begins with a single step”.
For me that single step is Binary Search, so let’s get started with it.
Searching
Searching/finding is the most elementary task that we do on daily basis e.g. searching a name in the phone book, searching a book on the bookshelf. The way we search an item majorly depends on how items are kept/arranged. For example, on a bookshelf, if books are kept haphazardly then one may have to check every book till he/she finds the desired book. But in case of the phone book, one can directly jump to the initials of the name.

In computer science, we are a handful of search algorithms. Some popular elementary search algorithms are Linear/Sequential Search, Binary Search, Interpolation Search, Ternary Search etc. Every search algorithm has it’s own pros and cons. In this post we’ll discuss a bit about Linear Search and then we’ll dive into Binary Search.
Linear/Sequential Search
In Linear Search as the name suggests we linearly/sequentially compare each item of the collection to the key item. We stop searching when we find the item else we continue searching until all the items are compared. Let’s take an example to understand it. Suppose we have been given a list of employee numbers in ascending order present on a particular day. We need to check whether employee 5 was present or not. We can leverage Linear Search to figure it out. We compare every id/number in the list with 5. If it’s found then we say that employee 5 was present else we’ll say employee 5 was absent. Here’s the implementation in javascript:
/**
* Linear Search.
* @param array
* @param element
*/
const linearSearch = (array, element) => {
// Traverse elements of the array and compare
// them
for (let i = 0; i < array.length; i++) {
// Compare element at ith position with
// key element. If both are equal then return
// the index.
if (array[i] === element) {
return i;
}
}
// no element found. Returns -1.
return -1;
};
const employees = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10];
const employeeId = 5;
const flagPresent = linearSearch(employees, employeeId) !== -1;
if (flagPresent) {
console.log(`Employee ${employeeId} was present.`);
} else {
console.log(`Employee ${employeeId} was absent.`);
}By looking at the number of comparisons we make to find the element using Linear Search, we can say that it’s time complexity is O(n) (You can read more about time complexity in my previous post An Ode to Asymptotic Notation) which means time taken by Linear Search is directly proportional to the size of the input.
We can conclude that Linear Search is good especially when input size is small but it’s sluggish when the input is relatively large. Also, it doesn’t take advantage of the fact that input i.e. employees list is sorted in ascending order. Let’s see if we can do better with Binary Search.
Binary Search
Binary Search is based on Divide and Conquer Technique. According to CLRS, Divide and Conquer technique is comprised of followings:
Divide: Break or divide the problem into the number of subproblems which are smaller instances of the same problem.
Conquer: Continue breaking the subproblems into smaller subproblems. If the subproblem size is small enough then solve it in a straightforward manner. Combine: the solutions of the subproblems into the solution for the original subproblems.
Binary Search repeatedly divides the problem into two subproblems that may contain the item. It discards one of the subproblems by utilising the fact that items are sorted. It continues halving the subproblems until it finds the item or it narrows down the list to a single item. Since binary search discards the subproblems because of that it’s pseudo Divide & Conquer algorithm. Here’s the pseudocode for binary search:
1. LET A is the list of items of size N and k is the key item.
2. LET min = 1 and max = N.
3. Repeat step 4, 5, 6 TILL min <= max.
4. LET mid = (min + max) / 2.
5. IF A[mid] === k THEN RETURN 'Item Found.'
6. IF A[mid] < key THEN SET min = mid + 1 ELSE SET max = mid - 1.
7. RETURN 'Item not found'.Here’s the JavaScript implementation for the same:
/**
* Iterative Binary Search Implementation
* @param array: array of items.
* @param key: key to be searched.
*
*/
const binarySearch = (array, key) => {
// Min and max for our beloved array.
let min = 0;
let max = array.length - 1;
while (min <= max) {
// Calculating mid for guessing and dividing the problem.
const mid = Math.floor((min + max) / 2);
if (array[mid] === key) {
// Yeah! key is present in the array. Let's return it's
// position.
return mid;
}
// Shifting mix and max respectively to focus
// on subarray which may contian key.
if (array[mid] < key) {
min = mid + 1;
} else {
max = mid - 1;
}
}
// We have reached here. It means key is not present in array.
// Let's return -1 as an indicator for "Not found".
return -1;
};The beauty of binary search is that in every iteration if it doesn’t find the key item, then it simply reduces the list to at least it’s half for the next iteration which makes a huge difference when we talk about its time complexity. Let’s consider worst-case scenario for an array of size 32. In the first iteration, we do not find the key element so we cut down the array length to 16. In next iteration, again we do not find the key element so again we cut it down to 8, then to 4, then to 2, and then to 1. Here’s the visual representation of Binary Search and Linear Search:

Complexity
The best case of binary search is when the first comparison/guess is correct(the key item is equal to the mid of array). It means, regardless of the size of the list/array, we’ll always get the result in constant time. So the best case complexity is O(1).
In worst case scenario, the binary search finds the item at the end of the list/array when it’s narrowed down to a single item. As we saw earlier with the list of size 32, to narrow it down to a single item we make at least 5 comparisons.
32/2 --> 16 // 1
16/2 --> 8 // 2
8/2 --> 4 // 3
4/2 --> 2 // 4
2/2 --> 1 // 5
Total = 5 guesses/comparisons.If we double the size to 64 then only one more comparison is extra made.
64/2 --> 32 // 1
32/2 --> 16 // 2
16/2 --> 8 // 3
8/2 --> 4 // 4
4/2 --> 2 // 5
2/2 --> 1 // 6
Total = 6 guesses/comparisons.If we look at the comparison and size of the input we see a pattern here eg. 32 = 2⁵ and 64 = 2⁶. Let’s assume n is the size of input and k is the number of comparisons then we can say that
Let’s apply logarithm to both sides with base 2(you can read more about logarithms here).
By the help of the equation above we can make a blanket statement that the worst case complexity of binary search is O(log n).
Limitations
- Binary search can be applied iff items are sorted otherwise one must sort items before applying it. And we know that sorting is relatively an expensive operation.
- Binary search can only be applied to data structures which allow direct access to elements. If we do not have direct access then we can not apply binary search on it eg. we can not apply binary search to Linked List.
Conclusion
Binary search is a powerful tool to find an element in a large collection especially when the collection is sorted and allows direct access to its element. We learned that for best-case binary search runs with constant time i.e. O(1) while for average and worst-case its runtime is O(log n).
Hi, I am Hitesh.