A Gentle Introduction to Trees 🌳

July 14, 2018 ∙ 📓 6 min

Most of the time when people embark upon the journey of learning data structures, they get started with linear data structures like array, stack, linked list, queue etc. And if the journey “continues”, they acquaint themselves with non-linear data structures like trees and graphs. Fortunately, I continued the journey and stumbled upon an infamous non-linear data structure called Tree. In this series of post, we’ll take a closer look at trees and different types of trees like Binary Tree, Binary Search Tree.

Let’s first understand linear and non-linear data structures before starting with trees.

Linear Data Structure:

“A data structure is a linear data structure if its data items(elements) form a sequence or a linear list”.

In plain English, linear data structures have a logical beginning and a logical end. Examples: array, stack, linked list, queue.

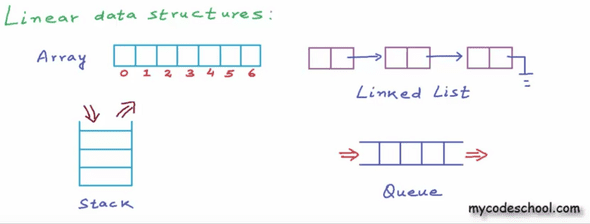
Non-Linear Data Structure:

Unlike linear data structures, elements of a non-linear data structure do not form a sequence because of that they can be traversed in any desired order or non-sequential order. Examples: Tree, Graph etc.

As a programmer, we often need to decide which data structure to use. Should we use a linked list ? or should we use a stack? Or Should we always use an array? Well, the choice of data structure depends upon the circumstances.

“Bad programmers worry about the code. Good programmers worry about data structures and their relationships.” ~ Linus Torvalds

One may take the following factors into considerations:

What needs to be stored ?
Memory usages or consumptions.
Ease of implementation.

Let’s address the elephant in the room. Trees are basically non-linear data structures which are mostly used to organize data in a hierarchical way. Let’s take some of the real life examples.

Here the Stark Family Tree from Game of Thrones.

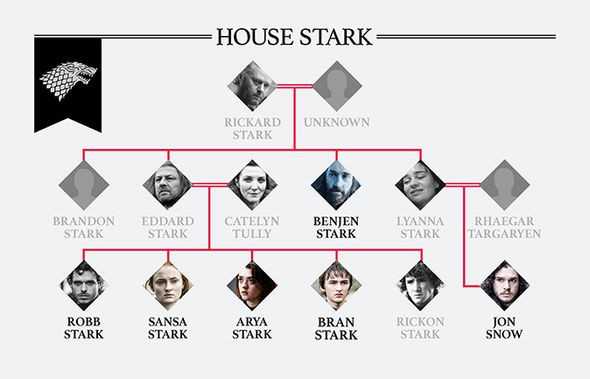
By looking at this tree, we can easily define relationships between each character.

We can say that Rickard and Unknown(yet to be revealed) are grandparents of Arya and her siblings i.e. Robb, Sansa, Bran, Rickon, and Eddard & Catelyn are their parents.

Also Arya and Jon Snow are cousin cause their parents are siblings. I hope Jon Snow at least knows this 😄.

Here’s another example which shows tree of a directory on file system.

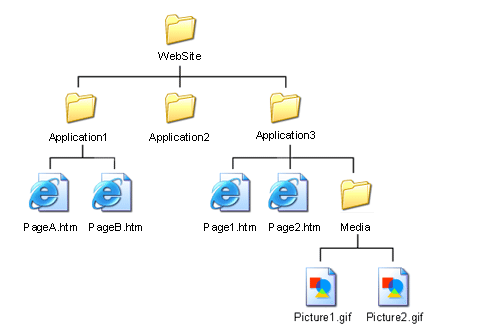
Tree Terminology:

 Sample tree
  -----------
       j    <-- root
     /   \
    f      k
  /   \      \  <-- edge
 a     h      z    <-- leaves

node: A basic entity in tree which can contain data or value and references to other nodes. We can say, a tree is collection of these nodes. In above sample tree j, f, k, a, h, and z are nodes of the tree.
root: is the top most node of a tree. j is the root node.
children: f and k are children of j. Similarly a & h are children of f while z is child of k.
parent: j is parent of f and k, and grandparent of a, h and z.
sibling: children which have same parent are called sibling. f and k are sibling. a and h are also siblings. But z is cousin of a and h cause their parents are siblings.
leaf: A node with no child is called leaf node. Here a, h and z are leaf node.
edge: Nodes are connected by edges. Sometimes edges are also referred as links.

Tree Properties:

Sample tree
   -----------
       j    <-- root - L-0
     /   \
    f      k         - L-1
  /   \      \
 a     h      z      - L-2

A tree with n nodes will have exacly n-1 edges or links (Tree with only root node has 0 link/edge). In the sample tree, we have 6 nodes and 5 edges (6 - 1).
The Depth of node x = length of the path from the root to node x. Length of a path is basically the number of edges in the path. So we can say that the depth of node x is the number of edges in the path from the root to x. The depth of the root node is 0. In the sample tree, depth of nodes f and k is 1, and depth of nodes a, h and z is 2. Nodes with the same depth have the same level the in tree. We can see f and k have the same depth and they are at the same level L-1.
The Height of node x = number of edges in the longest path from x to a leaf node. The height of a leaf node is 0 and the height of an empty tree is considered as -1. The height of a tree can be defined by the height of root node.

Note: In some books, the depth of a node x is referred to the number of nodes in the path from the root to node x. In that case, depth of the of the root node will be 1. Similarly, the height of the node x is also referred as the number of nodes in the longest path from node x to leaf node which means the height of leaf node will be 1 and height of empty tree will be 0 instead of -1. In this series of posts, we will consider this definition of height and depth. You can read detailed discussion on depth and height here.

Another notable property of trees which make them super-powerful is their recursive nature.

Yes, Trees are recursive in nature.

It means that a tree is composed of many small trees called subtree. If we ignore root node then every node in a tree represents a subtree. This property of trees helps us to write recursive algorithms for many operations like search and traversal, which are extremely simple to grok and implement.

Applications:

Here are some common uses of trees taken from Wikipedia.

Representing hierarchical data.
Storing data in a way that makes it efficiently searchable .
Representing sorted lists of data.
As a workflow for compositing digital images for visual effects.
Router algorithms.

Here’s a sample Tree class with a countLeaves method which counts the number of leaf nodes in a tree inspired by Raganwald post on stinking recursion.


class Tree {
  constructor(...children) {
    this.children = children;
  }
  countLeaves() {
    if (!this.children.length) {
      return 1;
    }
    return this.children.reduce((leaves, child) => {
      return leaves + child.countLeaves();
    }, 0);
  }
}
const tree = new Tree(new Tree(new Tree()), new Tree());
console.log(tree.countLeaves()); // 2 leaves

Hi, I am Hitesh.