A bit about Binary Heap 🌳

June 20, 2020 ∙ 👩🏻‍💻 7 min

We learned about trees and binary trees in posts A Gentle Introduction to Trees 🌳 and A Bit about Binary Tree 🌳. In this post, we’ll learn about a special type of binary tree called binary heap. A binary heap is a binary tree with following properties:

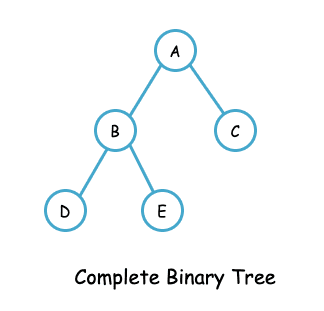
• A binary heap is a complete binary tree. In a complete binary tree, all levels are filled completely, except possibly the last level, and all nodes are as far left as possible.

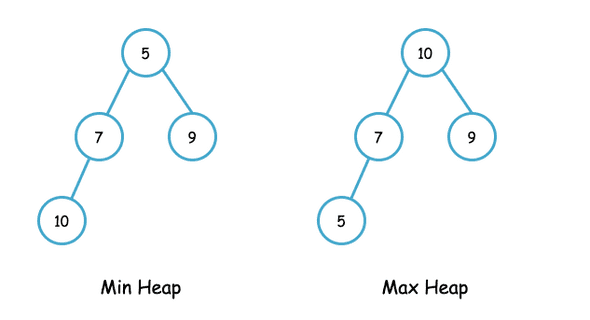
• The root element of a binary heap is minimum/maximum amongst other elements of the tree. This property makes a binary heap either min heap or max heap. The heap property is recursively true for all the subtrees in a binary heap.

A binary heap is typically implemented using an array. For an element at i^th position in array:

parent => (i - 1) / 2
left   => 2 * i + 1
right  => 2 * i + 2

Let’s quickly define operations for a binary heap.

• insert(item): inserts item to the heap.
• remove(i): removes the i^th item.
• getRoot(): returns the root element of the heap. It is getMin for MinHeap and getMax for MaxHeap.
• updateValue(i, value): updates the value of i^th item. It is decreaseValue for MinHeap and increaseValue for MaxHeap.
• size(): returns the size of heap.

We’ll use inheritance here, instead of composition because of is a relationship. We’ll define these methods in a base class BinaryHeap, which MinBinaryHeap and MaxBinaryHeap heap will extend. We’ll also make BinaryHeap class an abstract class with a comparator abstract method.

Copy
class BinaryHeap {
  constructor() {
    if (this.constructor === BinaryHeap) {
      throw new Error(
        `BinaryHeap is an abstract class. It can't be instantiated.`
      );
    }
    this._arr = [];
  }

  _swap(i, j) {
    [this._arr[i], this._arr[j]] = [this._arr[j], this._arr[i]];
  }

  _parent(index) {
    return Math.floor((index - 1) / 2);
  }

  _left(index) {
    return 2 * index + 1;
  }

  _right(index) {
    return 2 * index + 2;
  }

  _heapify() {
    // TODO: Provide stub.
  }

  comparator() {
    throw new Error('comparator method must be implemented');
  }

  insert(item) {
    // TODO: Provide stub.
  }

  remove(index, signedInfinity) {
    // TODO: Provide stub.
  }

  // Min heap -> `decreaseValue`
  // Max heap -> `increaseValue`.
  updateValue(index, value) {
    // TODO: Provide stub.
  }

  // Min heap -> `extractMin`
  // Max heap -> `extractMax`.
  extractRoot() {
    // TODO: Provide stub.
  }

  getRoot() {
    return this._arr[0];
  }

  size() {
    return this._arr.length;
  }
}

A MinBinaryHeap class which extends BinaryHeap.

Copy
class MinBinaryHeap extends BinaryHeap {
  constructor(comparator) {
    super();
    this.comparator = comparator || this.comparator;
  }

  comparator(a, b) {
    return a < b;
  }

  getMin() {
    return this.getRoot();
  }

  extractMin() {
    return this.extractRoot();
  }

  remove(index) {
    return super.remove(index, Number.NEGATIVE_INFINITY);
  }

  decreaseValue(index, value) {
    return this.updateValue(index, value);
  }
}

A MaxBinaryHeap class which extends BinaryHeap.

Copy
class MaxBinaryHeap extends BinaryHeap {
  constructor(comparator) {
    super();
    this.comparator = comparator || this.comparator;
  }

  comparator(a, b) {
    return a > b;
  }

  getMax() {
    return this.getRoot();
  }

  extractMax() {
    return this.extractRoot();
  }

  increaseValue(index, value) {
    return this.updateValue(index, value);
  }

  remove(index) {
    return super.remove(index, Number.POSITIVE_INFINITY);
  }
}

Let’s implement each operation for a min heap. Implementations of these operations for a max heap more or less remain same except the comparison of elements.

Insert

Insertion in binary heap is straight forward. We push the element to the array and swap it with its parent element until the heap property is satisfied.

For a min binary heap, one can use following steps for insertion:

1. Push element to the array.
2. While element is smaller than parent, swap parent and element.

Copy
class BinaryHeap {
  // other useful method
  // ...
  // ...

  insert(item) {    let pos = this._arr.length;    let parPos = this._parent(pos);    this._arr.push(item);    while (pos !== 0 && this.comparator(item, this._arr[parPos])) {      this._swap(parPos, pos);      pos = parPos;      parPos = this._parent(pos);    }    return this;  }
  // other useful methods
  // ...
  // ...
}

In the worst case scenario, the element moves from leaf to root of the binary heap. Consequently, the time complexity equals to the height of the heap i.e. O(logn).

Update

The update operation decreases/increases the value of a node for a min/max binary heap.

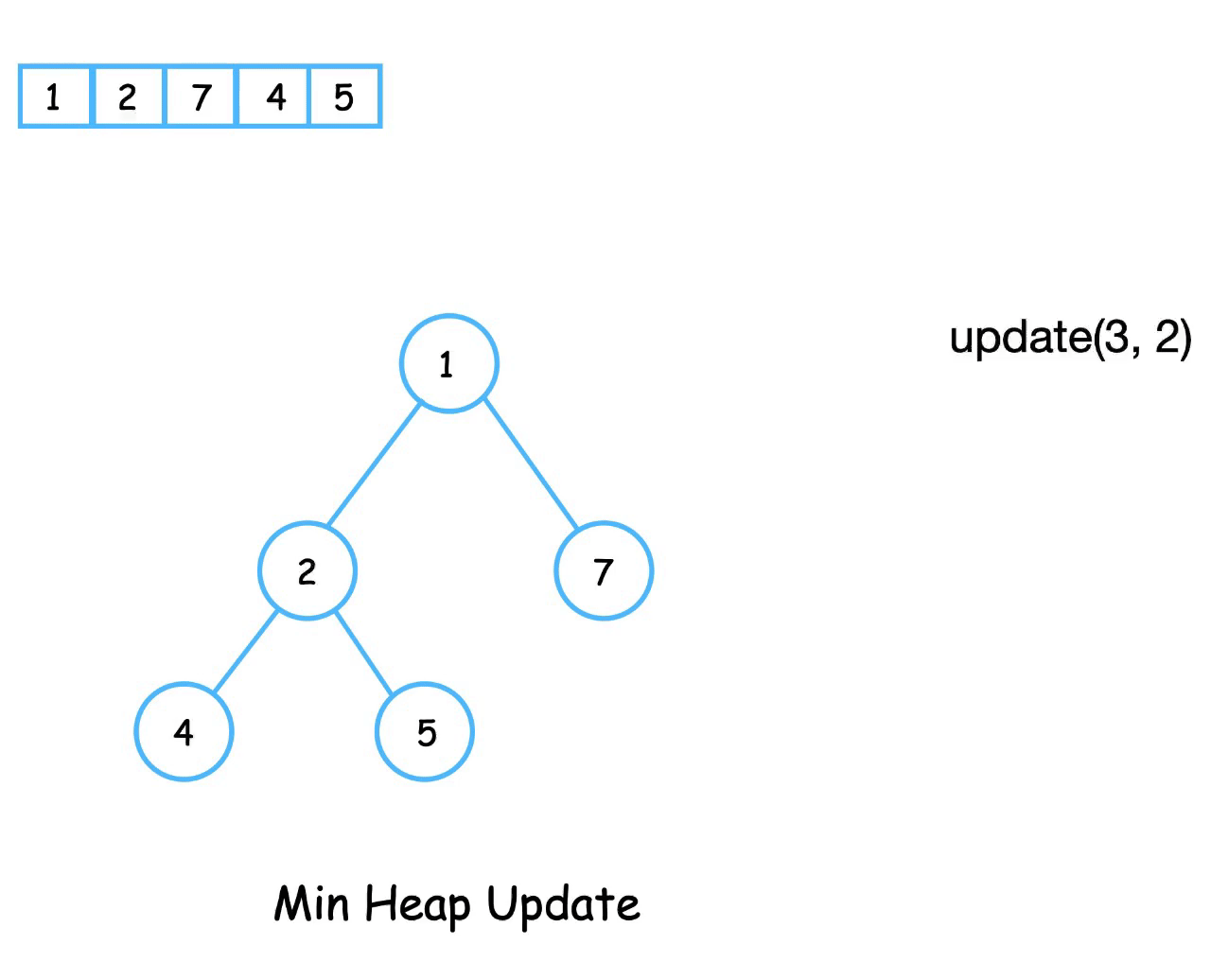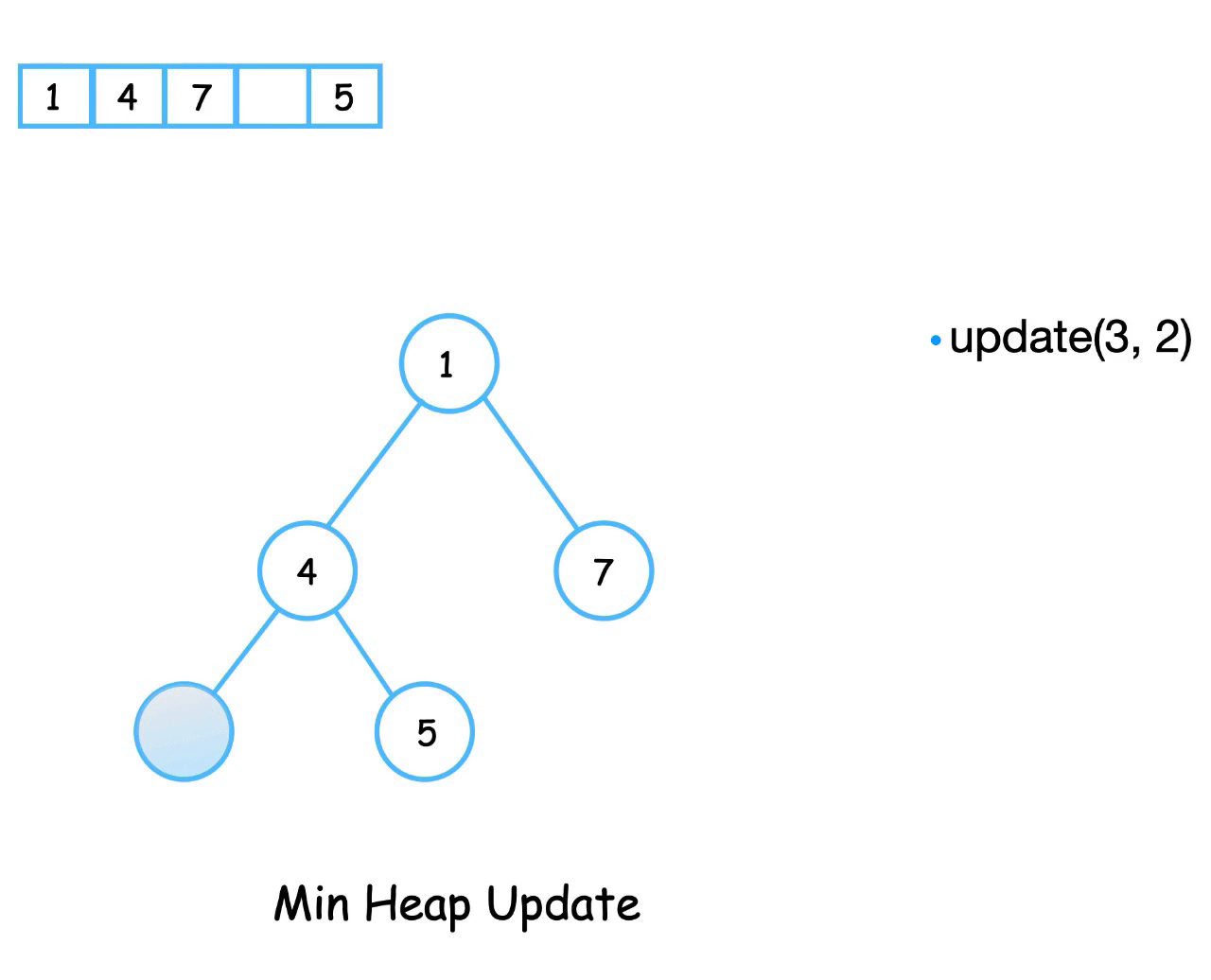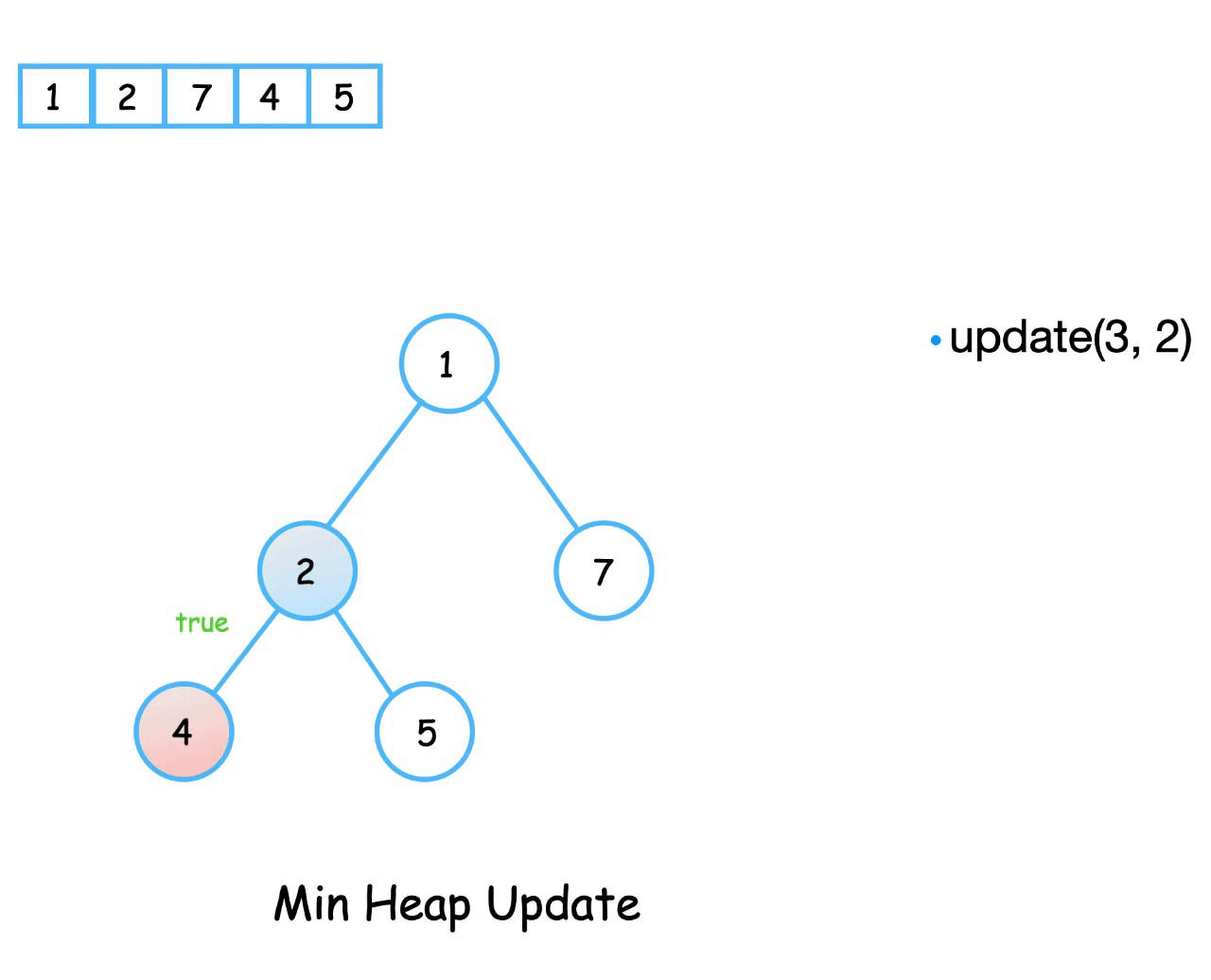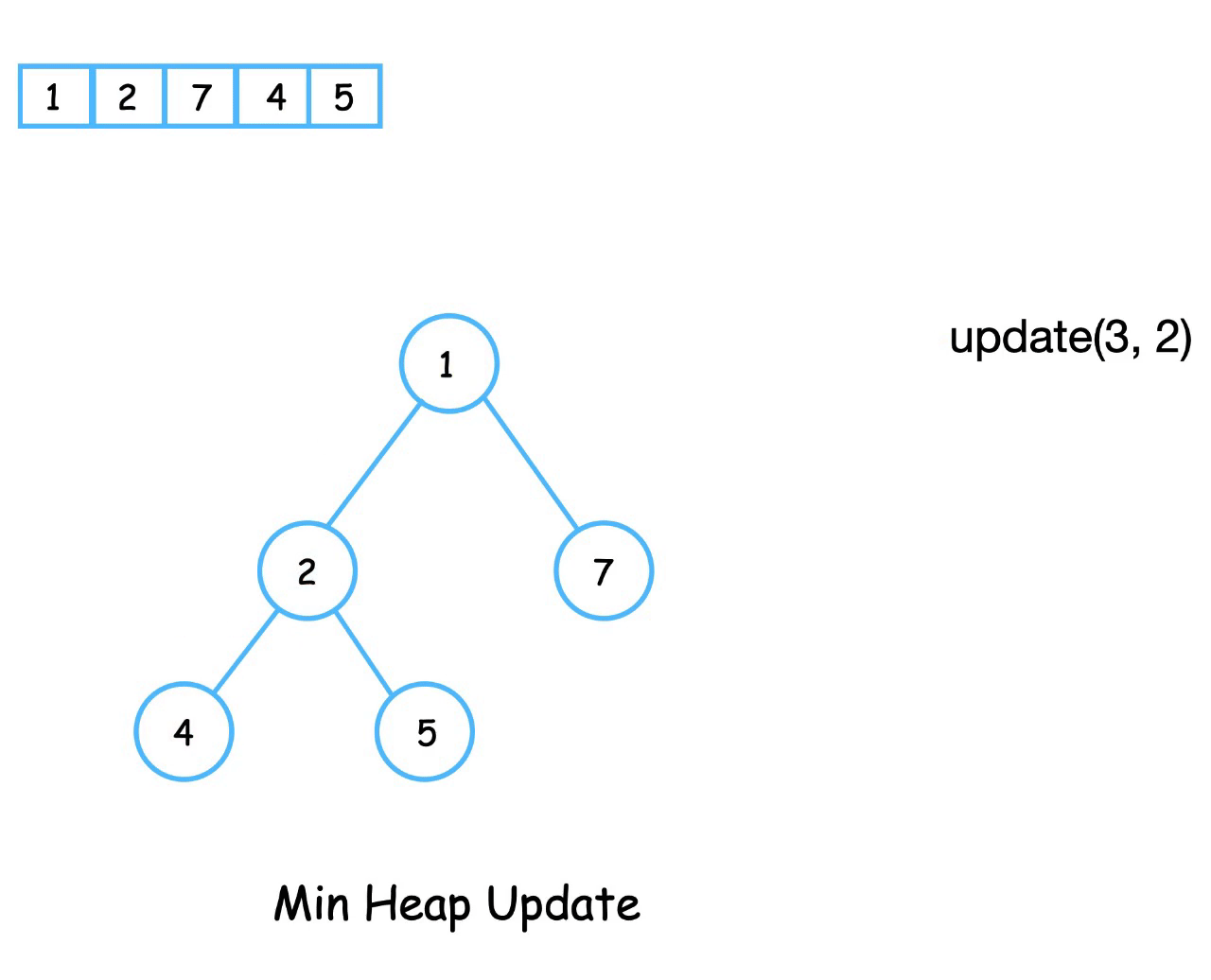
To update the value of node at position index, we replace it’s value with the new value and swap it with its parent element until the heap property is satisfied.

Copy
class BinaryHeap {
  // other useful method
  // ...
  // ...

  // Min heap -> `decreaseValue`  // Max heap -> `increaseValue`.  updateValue(index, value) {    this._arr[index] = value;    let pIndex = this._parent(index);    while (pIndex >= 0 && this.comparator(value, this._arr[pIndex])) {      this._swap(pIndex, index);      index = pIndex;      pIndex = this._parent(index);    }    return this;  }
  // other useful methods
  // ...
  // ...
}

The time complexity for update operation is O(logn)

Extract Root

The root element in the binary heap represents the maximum/minimum element. That’s why a min/max binary heap has an extractMin or extractMax method. Once the root is extracted, the elements of heap are rearranged or heapified to maintain the heap property.

To extract the root of a min binary heap, we replace the root with the farthest right leaf and heapify it.

To heapify a min heap, we find the minimum amongst the root and it’s children(left and right). If root is not the minimum element, then we swap it with the minimum element. We recursively follow this process till the heap property is satisfied.

Copy
class BinaryHeap {
  // other useful method
  // ...
  // ...

  _heapify(index) {    if (index >= this._arr.length) {      return;    }    let left = this._left(index);    let right = this._right(index);    let target = index;    if (      left < this._arr.length &&      this.comparator(this._arr[left], this._arr[target])    ) {      target = left;    }    if (      right < this._arr.length &&      this.comparator(this._arr[right], this._arr[target])    ) {      target = right;    }    if (target !== index) {      this._swap(target, index);      this._heapify(target);    }  }
  // Min heap -> `extractMin`
  // Max heap -> `extractMax`.
  extractRoot() {    if (this._arr.length === 0) {      return null;    }    if (this._arr.length === 1) {      return this._arr.pop();    }    const value = this._arr[0];    this._arr[0] = this._arr.pop();    this._heapify(0);    return value;  }
  // other useful methods
  // ...
  // ...
}

The time complexity to extract root is O(logn)

Delete/Remove

To delete an element from a binary heap, we update it’s value with maximum/minimum value i.e. Infinity and -Infinity and extract the root.

Copy
class BinaryHeap {
  // other useful method
  // ...
  // ...

  remove(pos, signedInfinity) {
    const v = this._arr[pos];
    this.updateValue(pos, signedInfinity);
    this.extractRoot();
    return v;
  }

  // other useful methods
  // ...
  // ...
}

The time complexity for deletion is O(logn).

Summary

Binary heaps are complete binary trees. Each node in a binary heap is minimum/maximum amongst its children(also known as heap property). Consequently, a binary heap can be either a min binary heap or a max binary heap.

A binary heap is typically implemented using an array. The parent, left and child element of the i^th element in array are present at (i - 1) / 2, 2 * i + 1, and 2 * i + 2 positions.

For a binary heap, basic operations like deletion, insertion, root extraction, etc take O(logn) time.

Hi, I am Hitesh.

|

• ← JavaScript and Bit-hacks 🧙🏻‍♂️
• How to "require" with aliases 🔁 →